Cryptography Basics

Cryptography is the core of many security mechanisms such as secret communication, message authentication, digital signature, exchanging secret keys, anonymous communication, electronic auction and election, digital cash, etc.

It is a common sense that cipher algorithms should be made public because open design allows a system to be scrutinized by many users, white hat hackers, academics and thus allows early discovery and correctness of flaws/vulnerabilities.

A cryptographic scheme is secure under some assumptions, that is against a certain type of attacker:

• Brute force: try all possible keys and it requires some knowledge about the structure of plaintext
• Ciphertext only attack: have access to some cipher text c1, ..., cn
• Known plaintext attack: some plaintext/ciphertext pairs (m1,c1), (m2,c2)...st. ci=E(k,mi)
• Chosen plaintext attack: an encryption oracle to encrypt messages m1...mn of his choice
• Chosen ciphertext attack: a decryption oracle to decrypt ciphertext c1...cn of his choice
• Unlimited or realistic $\le 2^{80}$ computational power

Symmetric cipher

Encryption algorithm E and Decryption algorithm D st. $$\forall k \in K \text{ and } \forall m \in M, \quad D(k, E(k, m)) = m$$

One-Time Pad (OTP, 1917)

XOR operator applied bitwise to two equal-length binary string.

Encryption: $C = M \oplus K$

Decryption: $M = C \oplus K$

Consistency is due to the associative property of XOR.

Perfect secrecy: for all messages $m_1,m_2 \in M$ of same length and for all ciphertext $c \in C$: $$|Pr(E(k, m_1)=c) - Pr(E(k,m_2)=c)| \leq \epsilon$$ where $\epsilon$ is some negligible quantity.

OTP satisfies perfect secrecy because

$$\begin{align} Pr(E(k,m)=c) &= \frac{\#\{k \in K: k \oplus m=c\}}{\#K} \\ &= \frac{1}{\#K} \end{align}$$

Limitations:

• key/pad is as long as the plaintext
• key should be completely random
• subject to two-time pad attacks (i.e., reuse a one-time pad)
  • given $m_1 \oplus k$ and $m_2 \oplus k$
  • can compute $m_1 \oplus m_2$ = $(m_1 \oplus k) \oplus (m_2 \oplus k)$
  • frequency analysis will reveal $m_1,m_2$
• are malleable
  • given the ciphertext c = E(k,m) with m = 'to bob:m0'
  • can compute the ciphertext c' = E(k,m') with m' = 'to eve:m0'
  • $c^\prime:=c \oplus \text{to bob:00...00} \oplus \text{to eve:00...00}$

Stream cipher

Stream cipher makes OTP practical by using a pseudorandom key rather than a really random key. The key is generated from a key seed using a pseudo-random generator (PRG): $\{0,1\}^s \to \{0,1\}^n \quad s \ll n$.

• doesn't satisfy perfect secrecy
• still subject to two-time pad attack and are malleable.

Properties of PRG:

1. it should be hard to predict a number from its preceding number
2. pseudo-random sequence is generated deterministically from a random seed and will start repeating itself at some point. The number of values that are output by the sequence before it repeats is known as its period

Below are 2 specific PRG and some week stream ciphers based on them.

• RC4
  • WEP uses RC4
• Linear feedback shift registers (LFSRs)
  • Content Scrambling System (CSS) uses LFSRs

Block cipher

Encryption: $\{0,1\}^k \times \{0,1\}^l \to \{0,1\}^l$

Decryption: $\{0,1\}^k \times \{0,1\}^l \to \{0,1\}^l$

DES (1970)

k=56 bits, l=64 bits

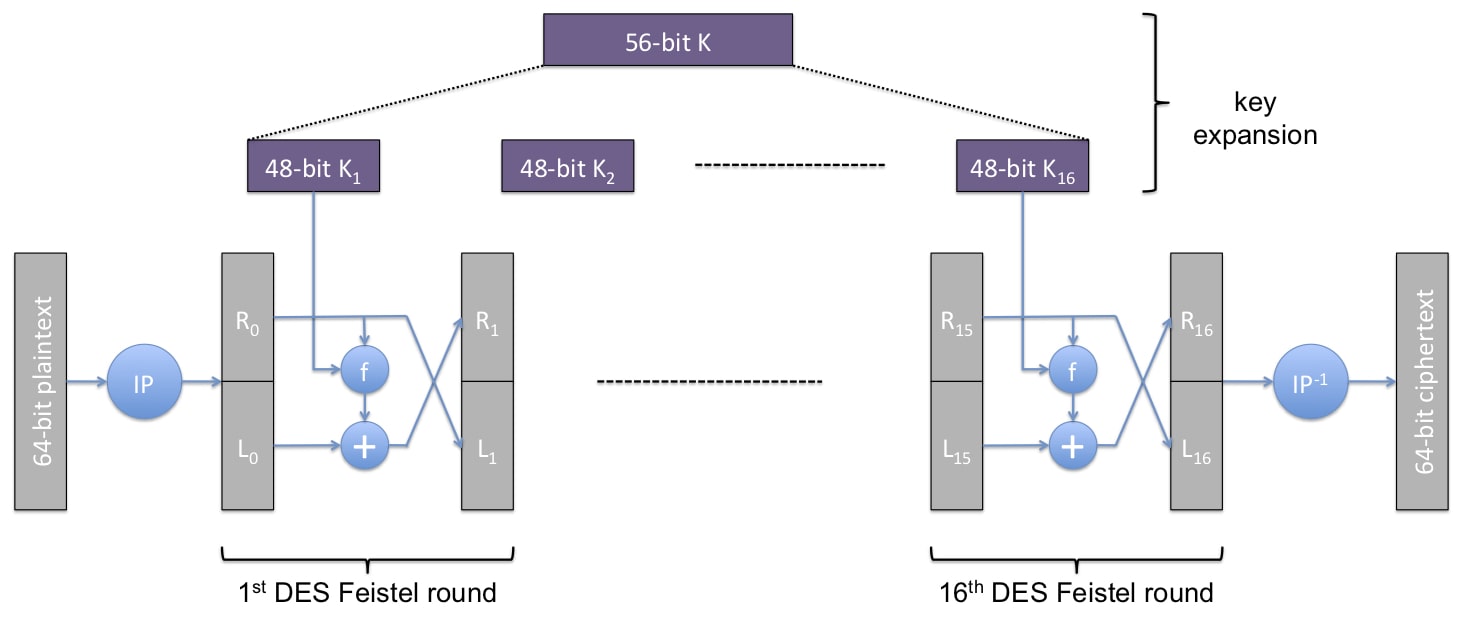
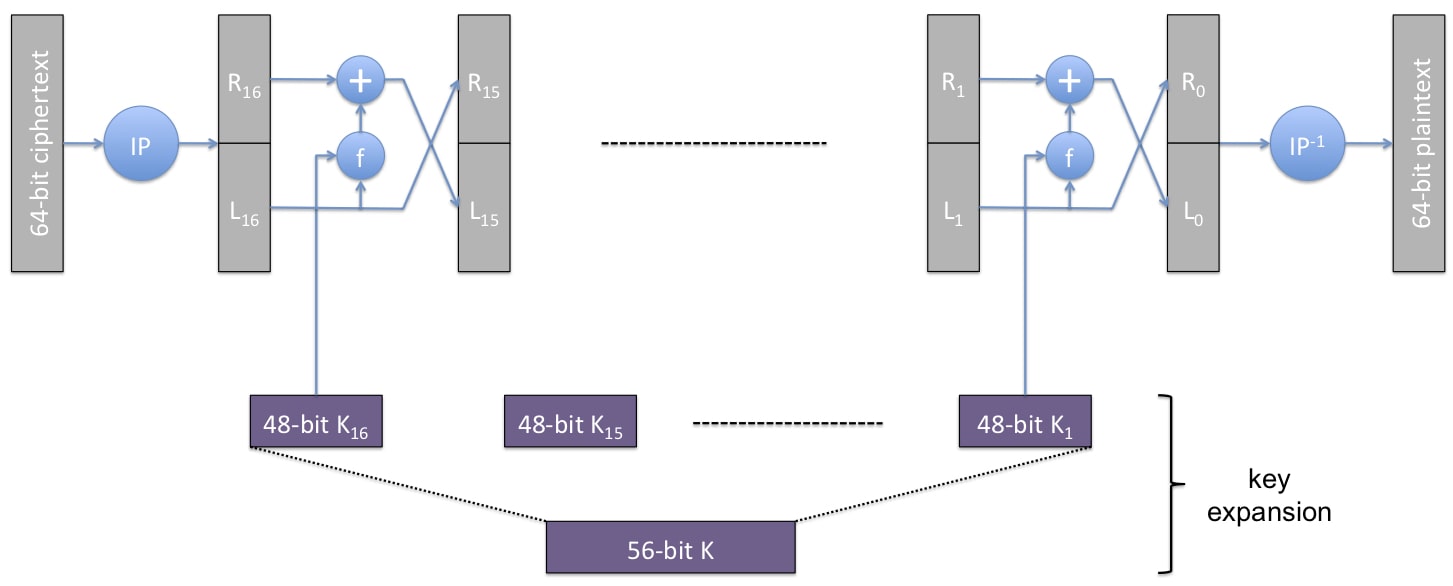
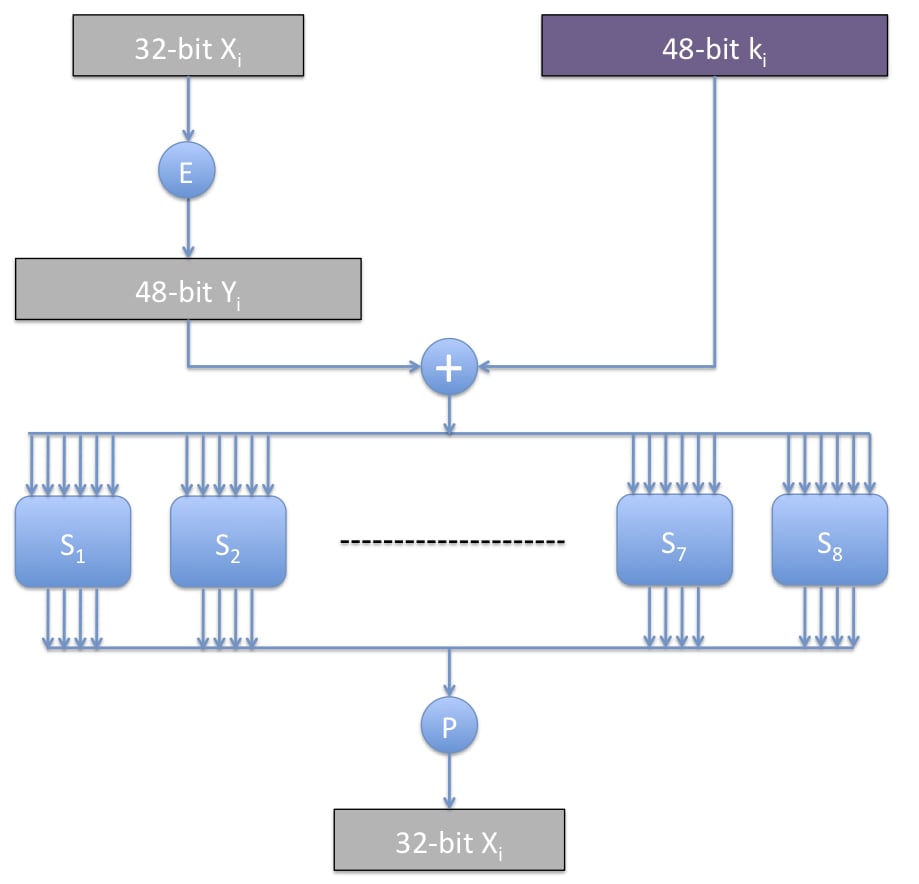
Each Feistel round is invertible. However, the function f or $S_5$ is not invertible because it maps 6 bits to 4 bits.

DES is not secure:

• exhaustive search: $2^{56}$
• linear cryptanalysis: found affine approximation to DES in time $\approx 2^{43}$
  1. can find 14 key bits in time $2^{14}$
  2. brute force the remaining $2^{42}$

Triple DES (3DES)

$E_{3DES}/D_{3DES}: (\{0,1\}^k)^3 \times \{0,1\}^l \to \{0,1\}^l$

$$E_{3DES}((K_1,K_2,K_3), M) = E_{DES}(K_1,D_{DES}(K_2,E_{DES}(K_3,M)))\\ D_{3DES}((K_1,K_2,K_3), C) = D_{DES}(K_3,E_{DES}(K_2,D_{DES}(K_1,M)))$$

Secure but 3 times as slow as DES:

• Exhaustive search attack: $2^{168}$ because Key-size = $3 \times 56 = 168$ bits
• meet-in-the-middle attack: $2^{118}$

AES (1997)

Block size l=128 bits, Key size k=128,192,256 bits

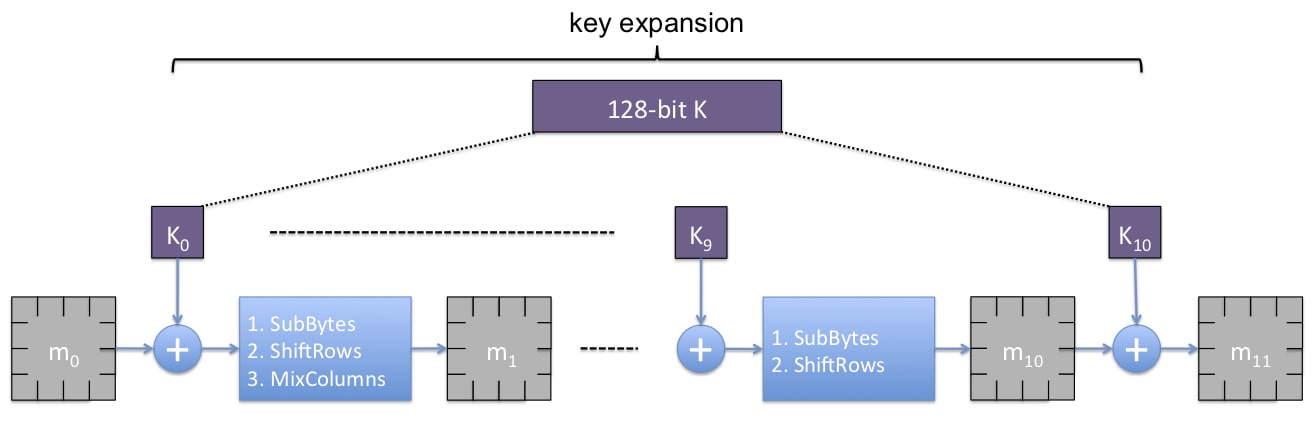
• $K_i$: 128 bit key
• $m_i$: 4X4 byte matrix, called state. $m_0$ is plaintext, $m_{11}$ is ciphertext

Each round consists of the following 4 basic steps (at the last round, MixColumns is not applied) and each step is invertible:

1. AddRoundKey
2. SubBytes
3. ShiftRows
4. MixColumns

Although existing attack on AES-128 is not practical, it's still recommended to use AES-192 or AES-256 instead.

Modes

What if the length of message M is not l?

M is padded: $M^\prime = M \| P$ such that $|M^\prime| = m \times l$

• bit padding: append a set bit 1 at the end of message and then append as many reset bits 0 as required
• byte padding: pad with zeros except the last byte defines the total number of padded bytes

There are various ways to use block cipher known as modes of operation.

• ECB (Electronic CodeBook): $M^\prime$ is broken into m blocks of length l and each block is encrypted using the block cipher. The ciphertext is the concatenation of all the $C_i$s. $$C_i = E_K(B_i) \\ B_i = D_K(C_i)$$
  • tolerant to the loss of a block
  • deterministic: identical blocks will have identical encryptions therefor ECB may reveal information in the stream of blocks and weak to frequency analysis. E.g., encrypted image reveal pattern in the original image
  • malleable, e.g., PlayStation disk encryption broken
• CBC (Cipher-Block Chaining): $$C_i = E_K(B_i \oplus C_{i-1}) \\ B_i = D_K(C_i) \oplus C_{i-1}$$
  • avoid the revelation of patterns in a sequence of blocks because identical blocks that appear at different places in the input sequence are very likely to have different Encryption blocks in the output.
  • the input blocks must be encrypted sequentially but decryption can be proceed in parallel
• CTR (Counter): $$V_i = E_K(seed+i-1) \\ C_i = V_i \oplus B_i \\ B_i = V_i \oplus C_i$$
  • the generation of initialization vector, every step of encryption and decryption can be done in parallel
  • recover from dropped blocks

Asymmetric cipher / Public-Key cryptography

$$\forall (pk,sk) \in G \text{ and } \forall m \in M, D(sk, E(pk, m)) = m$$

The encryption key pk is known to everyone and the decryption key sk is secret.

Each PKC algorithm is based on some intractable problem.

Block of bits are viewed as large numbers. Arithmetic operations are applied to these numbers to perform encryption and decryption. All operations are followed by Modular n to ensure the result is a value in $Z_n = \{0, 1, \cdots, n-1\}$.

Number theory

$$Z_n = \{0, 1, \cdots, n-1\} \\ \forall b \in Z_n, a \equiv b \pmod{n} \iff \exists k \in \mathbb{N}. a=b+kn$$

$$Z_n^* = \{x|x \in Z_n \text{ and } \gcd(x,n)=1 \} \\ \phi(n) = |Z_n^*|$$

Euler's Theory: $\forall x \in Z_n^*, x^{\phi(n)} \equiv 1 \pmod{n}$

Corollary: $\forall$ prime p, $Z_p^*$ is a cyclic group, i.e., $\exists g \in Z_p^*, Z_p^*=\{g^0, g^1, \cdots, g^{n-2}\}$ where g is said to be a generator

$y \in Z_n$ is the inverse of $x \in Z_n$, denoted $x^{-1}$, if $xy \equiv 1 \pmod{n}$

Theorem: Let $x \in Z_n$, x has an inverse in $Z_n$ iff gcd(x, n)=1

RSA

algorithm

1. Key generation:
   1. pick 2 large random primes p, q and set n=pq
   2. pick a number e which is relatively prime to $\phi(n)$, pk=(e, n)
   3. compute $d = e^{-1} \text{ mod } \phi(n)$, sk=(d, n)
2. Encryption: $C = M^e \text{ mod } n$
3. Decryption: $M = C^d \text{ mod } n$

correctness proof is based on number theory mentioned above: [todo]

security is tied to the following 2 hard problems:

1. RSAP: input pk=(e,n) and $c=m^e \pmod{n}$, output m
2. factoring: input n, output primes p1,...,pm st. n=p1...pm

   Theorem: every $n \in \mathbb{N}$ has a unique factorization as a product of prime numbers (factors)

However, raw RSA $(G_{RSA}, RSA, RSA^{-1})$ is not secure against chosen plaintext attack. The recommended ISO standard combines asymmetric and symmetric encryption and hash function together: 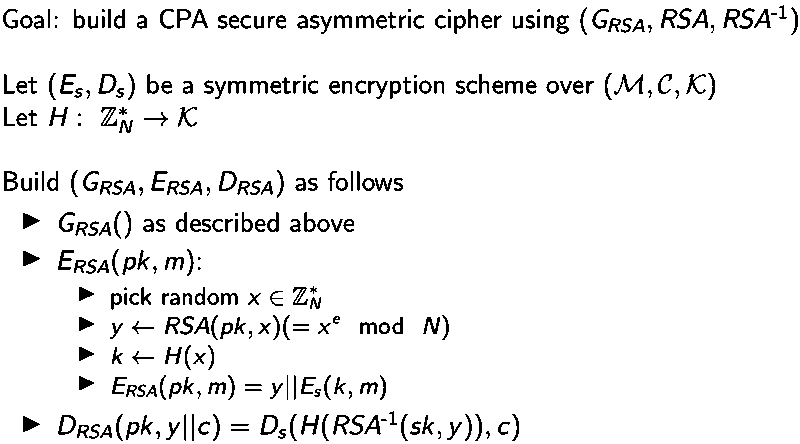Besides, RSA is homomorphic which means it's vulnerable to forgeability.

Elgamal

Algorithm is as follows:

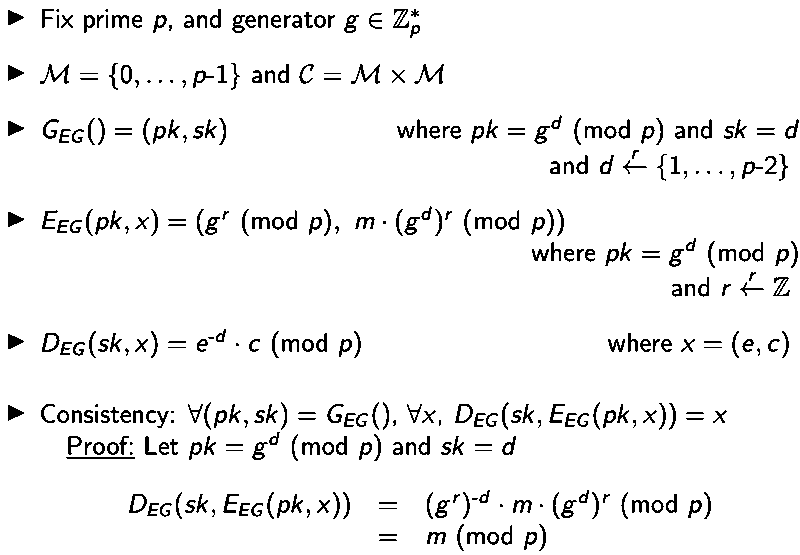
Security is based on Discrete Logarithm problem: input prime p, generator g of $Z_p^*, y=g^x \pmod{p}$, output x

• Advantage: independent encryption of the same plaintext produce different ciphertext due to the use of randomness.
• Disadvantage: vulnerable to forgeability and chosen cipher text

Comparison of symmetric and asymmetric encryption

• Symmetric encryption scheme uses the same key (secret) to encrypt and decrypt whereas asymmetric encryption scheme has a public key for encryption and a private key for decryption or vice versa.
• Symmetric ciphers are much faster and thus suitable for encrypting large files while Asymmetric ciphers tend to be computationally more expensive
• Public key cryptography is reused for a long time while symmetric key is usually generated on the fly: long-term asymmetric keys are usually used to establish short-term shared/symmetric secret keys

Key agreement/exchange protocol

Besides asymmetric cipher like RSA, some protocols below are also able to establish a shared secret key.

Diffie-Hellman

DH key exchange protocol is not a PKC but aims to establish a shared secret key instead.

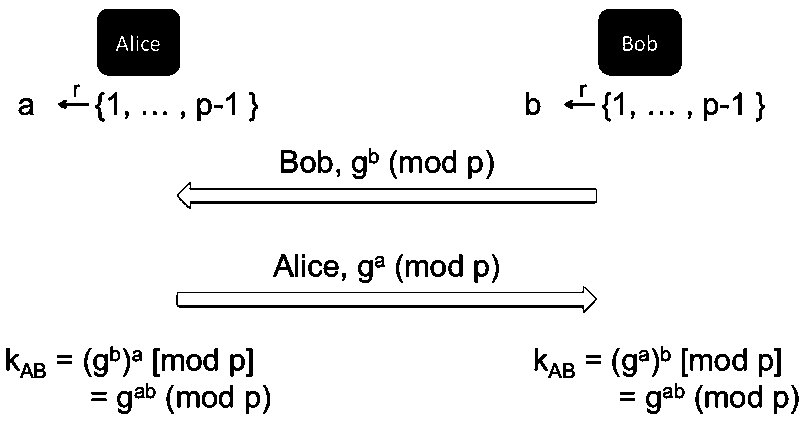
security is based on:

• Discrete Logarithm: difficult to recover x from $X=g^x \pmod{n}$
• Diffie-Hellman: input prime p, generator g, $X=g^x \pmod{p}$ and $Y=g^y \pmod{p}$, output $K=g^{xy} \pmod{p}$

security properties:

• secure against a passive eavesdropper
• provide forward secrecy

  A protocol ensures forward secrecy if even the long-term keys are compromised, past sessions are still kept confidential.

• vulnerable to an active man-in-the-middle attacker who can modify the message

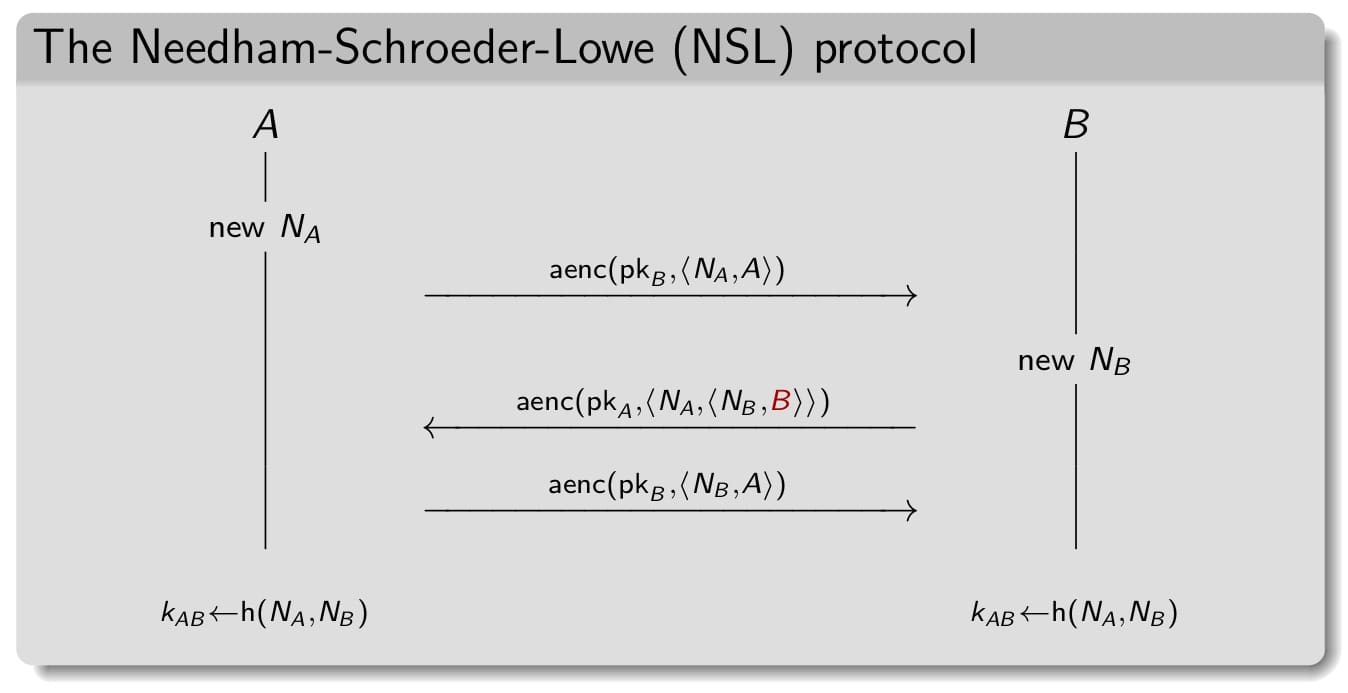
NSPK (1978)

Needham Schroeder Public Key looks a bit like three-handshake in TCP establishment.

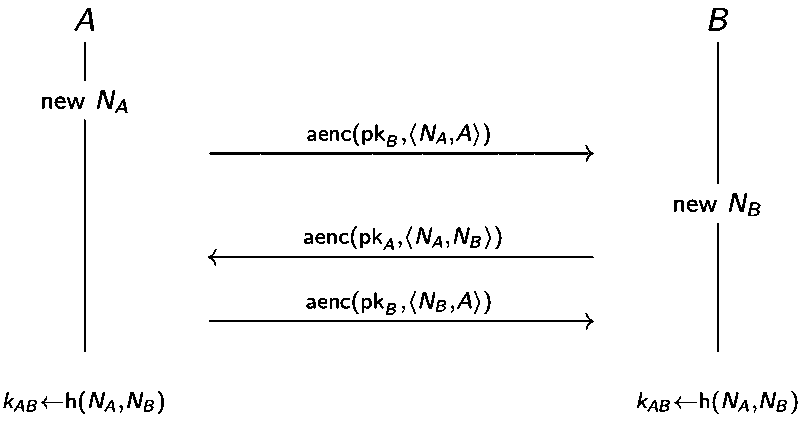
Attack found 17 years after the publication and its corresponding fix:

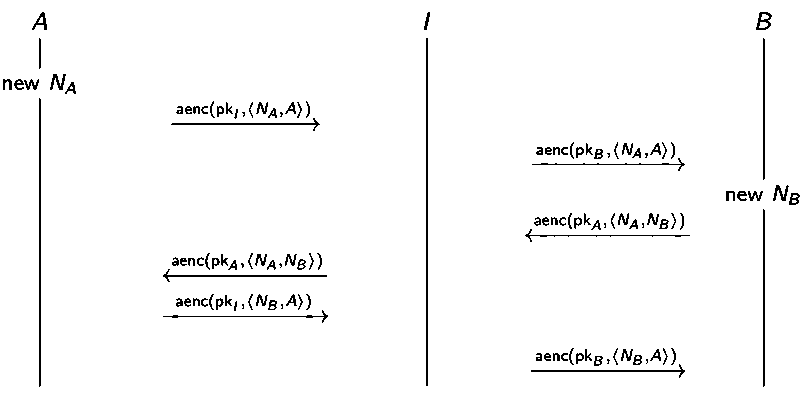
StS

The Station-to-Station (StS) protocol ensures mutual authentication, key agreement and forward secrecy.

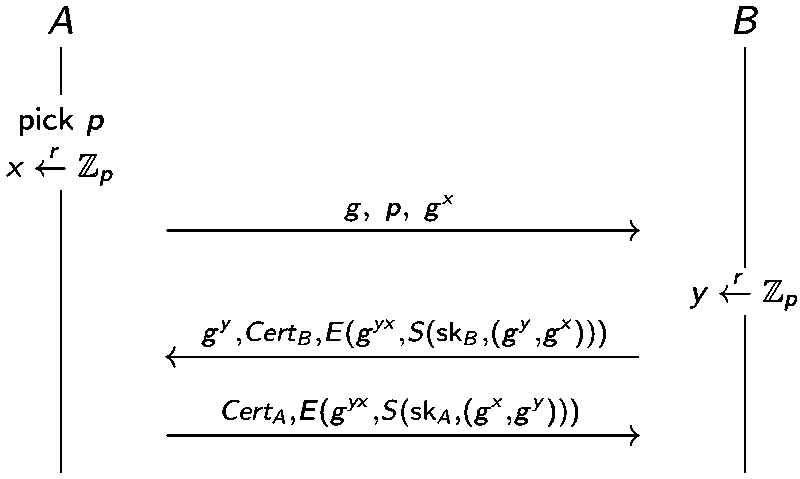
It is similar to DH but also relies on the certificate and signature to avoid MitM attack.

BAC

The Basic Access Control protocol is the key agreement protocol implemented in e-Passports.

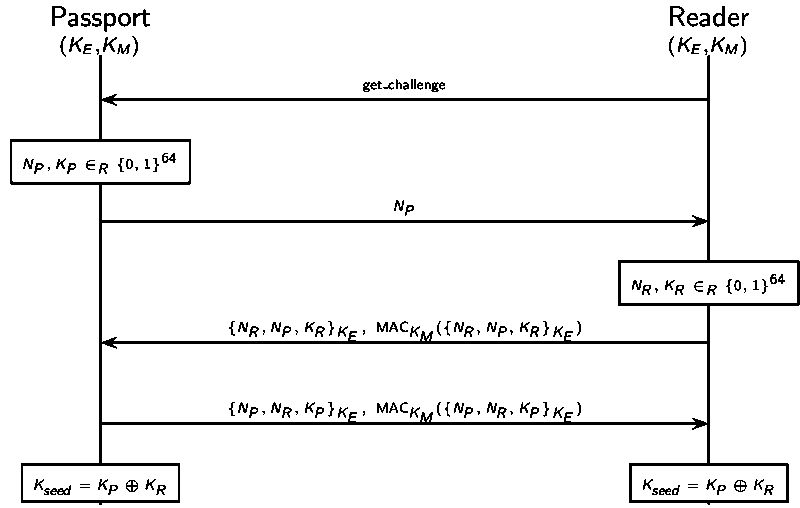The e-Passport is embedded with a RFID tag which contains the information printed on the passport. The reader can read the secret keys directly from the passport. Subsequent communication is done through RFID, which might be intercepted/recorded by an attacker and used to perform replay attack later.

The problem is that the passport must reply to all received messages and indicate mac_err or nce_err on error.

Below is an attack on the anonymity on French e-Passport where mac_err ≠ nce_err

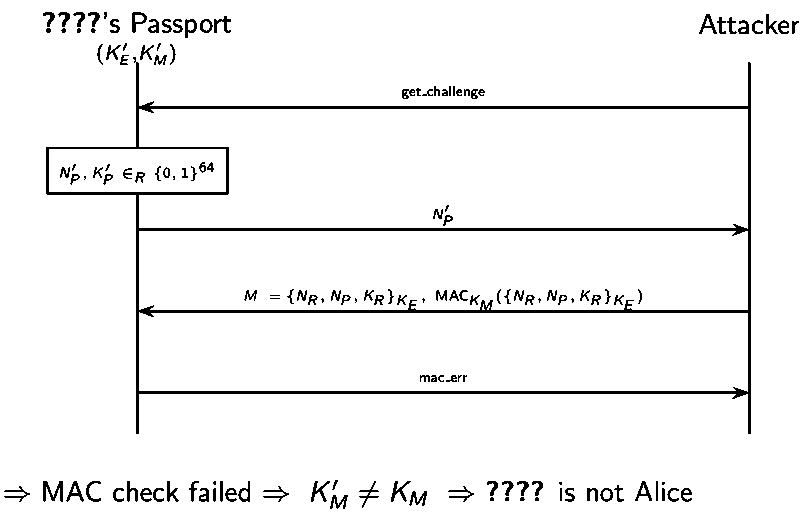
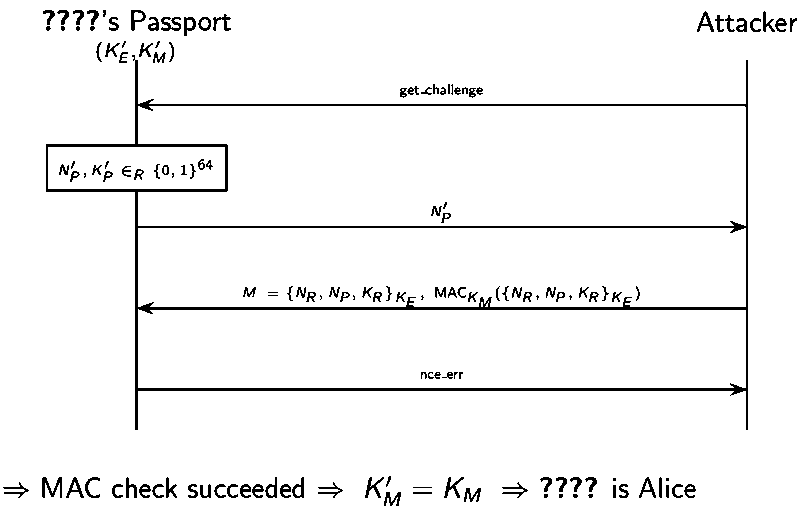
Timing attack is also possible based on the fact that failed MAC check is rejected sooner.

Hash function

Hash function $H:M \to \{0,1\}^n, |M| >> 2^n$ can produce a compressed digest of a message. That is, it is a mapping from a message of arbitrary length to a fixed-size binary string. It has the following properties:

1. one-way: hard to retrieve a message from its hashed value
2. collision-resistant: hard to find 2 different messages with the same hash value. Therefore, any change to the data will change the corresponding hash value

Applications:

• commitment
• file integrity
• password verification

Merkle-Damgard

Both hash function MD5 and SHA256 follow MDP construction.

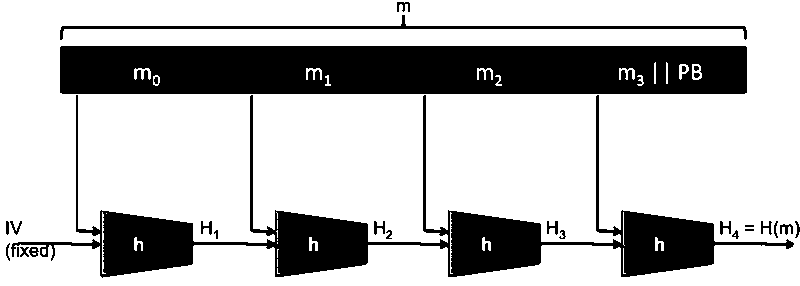
compression function h is usually built from a block cipher and the details are omitted here.

Theorem: Let H be built using compression function h under the MD construction. If H admits a collision, so does h.

Birthday attack

What?

Birthday attack is a kind of attack aimed to compromise the collision resistance based on a nonintuitive phenomenon that states:

if there are more than 23 people in a room, there is better than 50% chance that two of the people have the same birthday.

It implies that there is 50% chance to find a collision in time $O(2^{n/2})$. Therefore, A hash function with 256-bit output value has 128-bit security.

Why?

1. the probability that the i-th message does not collide with the previous i-1 messages is $1-\frac{i-1}{m}$ where $m=2^n$
2. the probability that the attacker has not found any collision after generating k messages is $F_k = (1-\frac{1}{m}) \times (1-\frac{2}{m}) \cdots (1-\frac{k-1}{m})$
3. the attacker succeed with 50% probability when $F_k = \frac{1}{2}$
4. solve for k: $k \approx 1.17 \sqrt{m}$

How?

1. Choose $2^{n/2}$ random messages in $M: m_1, \cdots, m_{2^{n/2}}$
2. Compute $t_i = H(m_i)$
3. If there exists a collision $(t_i=t_j)$, return $(m_i, m_j)$ else go back to 1

MACs

Message Authentication Codes is another way to ensure message integrity as well as authentication.

A MAC is a pair of algorithms (S, V) defined over (K, M, T):

• S: $K \times M \to T$
• V: $K \times M \times T \to \{\top, \bot\}$
• Consistency: V(k, m, S(k, m)) = T

Algorithms:

• ECBC-MAC
• PMAC
• HMAC $$HMAC(k,m) = H(k \oplus OP || H(k \oplus IP || m))$$

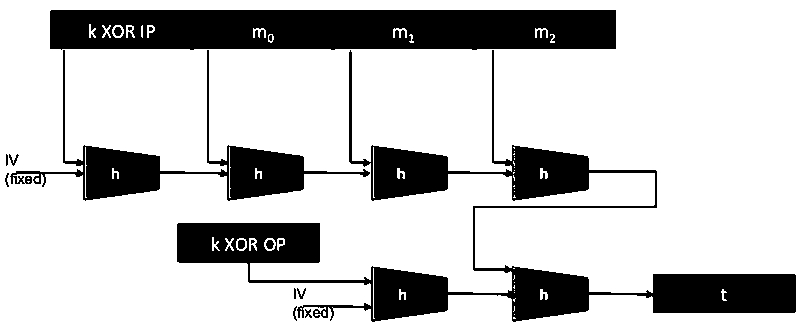
When do we use MACs?

Decryption never fails even if one bit of the ciphertext is modified. However, we want to avoid decryption if ciphertext is modifed by using Encryption-then-MAC:

Encryption:

1. $C \gets E_{AES}(K_E, M)$
2. $T \gets HMAC(K_M, C)$
3. return $C \| T$

Decryption:

1. if $T = HMAC(K_M, C)$
2. return $D_{AES}(K_E, C)$
3. else return $\bot$

Digital signature

A digital Signature is a way to demonstrate authenticity using public key cryptography.

$$\forall(sk,vk) \in G \text{ and } \forall m \in M, V(vk, S(sk, m))=m$$

Digital signature schemes are usually applied to cryptographic hashes of messages, not the actual messages for practical and secure reason: 1. more efficient 2. unforgeability.

RSA signature:

1. digital signing: encrypt the hash value of the message using private key $$S_{RSA}(sk, x) = (x, H(x)^d \pmod{p})$$
2. signature verification: decrypt the signature with public key and compare it with the hash value of the message $$V_{RSA}(pk, x, s) = \begin{cases} \top,& \text{if } H(x)=s^e \pmod{p} \\ \bot,& \text{otherwise} \end{cases}$$

Properties:

• non-forgeability: difficult for an attacker, Eve, to forge the signature for a message as if it is coming from Alice
• non-repudiation: it is also difficult for Alice to deny it if she signs a document with her private key

Advantages over MAC

• publicly verifiable
• non-repudiation

Anonymity

Anonymity means

A user may use a service without disclosing the user's identity

Anonymity can be achieved by hiding one's activities among others' similar activities.

Dining cryptographers

Problem definition: Three cryptographers are having dinner. Either NSA paid for the dinner or one of the cryptographers. They want to figure out whether it is that NSA paid but without revealing the identity of the cryptographer that paid in the case that NSA did not pay.

3DC protocol:

1. Each cryptographer flips a coin and shows it to his left neighbor
2. Each cryptographer announces whether the his own coin and his right neighbor's coin are the same. If he is the payer, he lies
3. odd number of "same" -> the NSA paid; even number of "same" -> one of the cryptographers paid. Only the one who paid knows he is the payer.

Let's consider a general scenario, the sender wants to broadcast a message within a group of size n:

1. for each bit of the message, every user generates a random bit and sends it to his left neighbor. every user learns two bits: his own bit and his right neighbor's bit
2. every user (except the sender) announces (own_bit XOR neighbor's_bit)
3. the sender announces (own_bit XOR neighbor's_bit XOR message_bit)
4. message_bit = XOR all announcements. Why? every randomly generated bit occurs twice and is thus cancelled by XOR while message bit occurs only once

Limitations:

• require pair-wise shared secret keys to share random bits
• require large amount of randomness

Crowds

randomly route the request through a crowd of users.

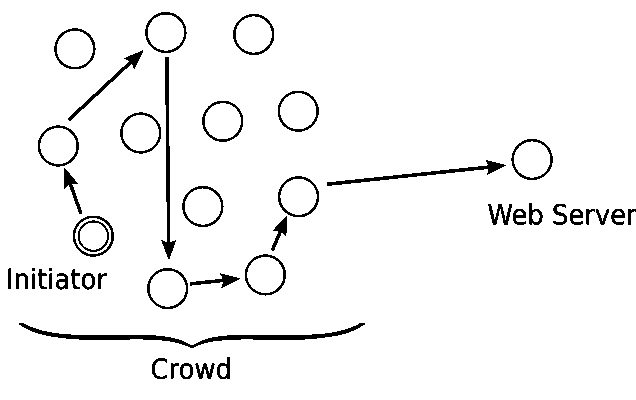
An initiator that wants to request a webpage creates a path from him to the server:

1. select a forwarder from the crowd and sends him the request
2. a forwarder forwards the request to a randomly selected new forwarder with probability p (the new forwarder repeats this procedure) or delivers the request directly to the server with probability 1-p.
3. the response from the server follows the same route in opposite direction

Limitation: not secure against an attacker that sees the whole network traffic

Chaum's mix

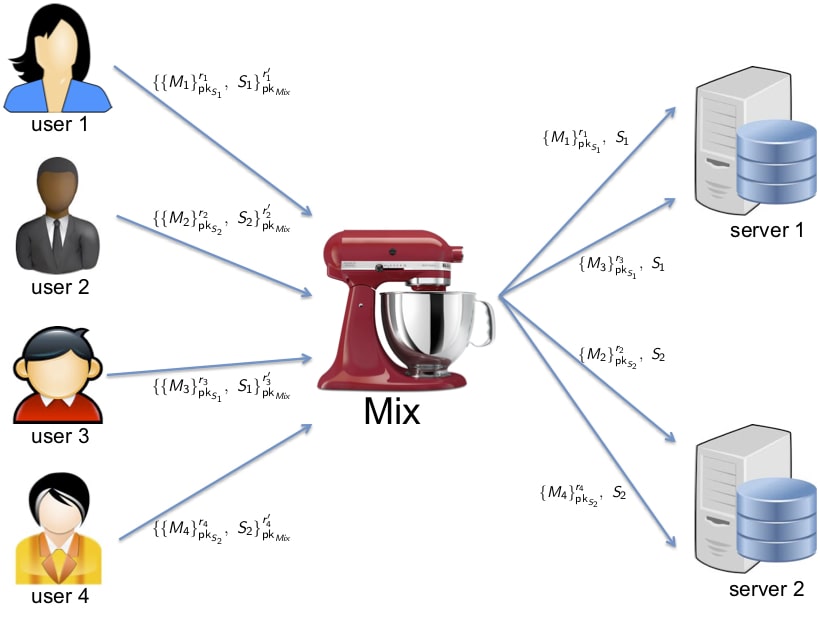
Messages can be sent through a sequence of mixes (Mix cascade). A single honest mix can guarantee anonymity against an attacker controlling the whole network if it applies the following measures to avoid time and volume correlation attack:

• message padding
• buffering
• dummy messages

Limitation: asymmetric encryption, buffering and dummy messages are inefficient

Onion routing

Onion routing combines advantages of mixes and proxies. An example of onion routing is Tor browser:

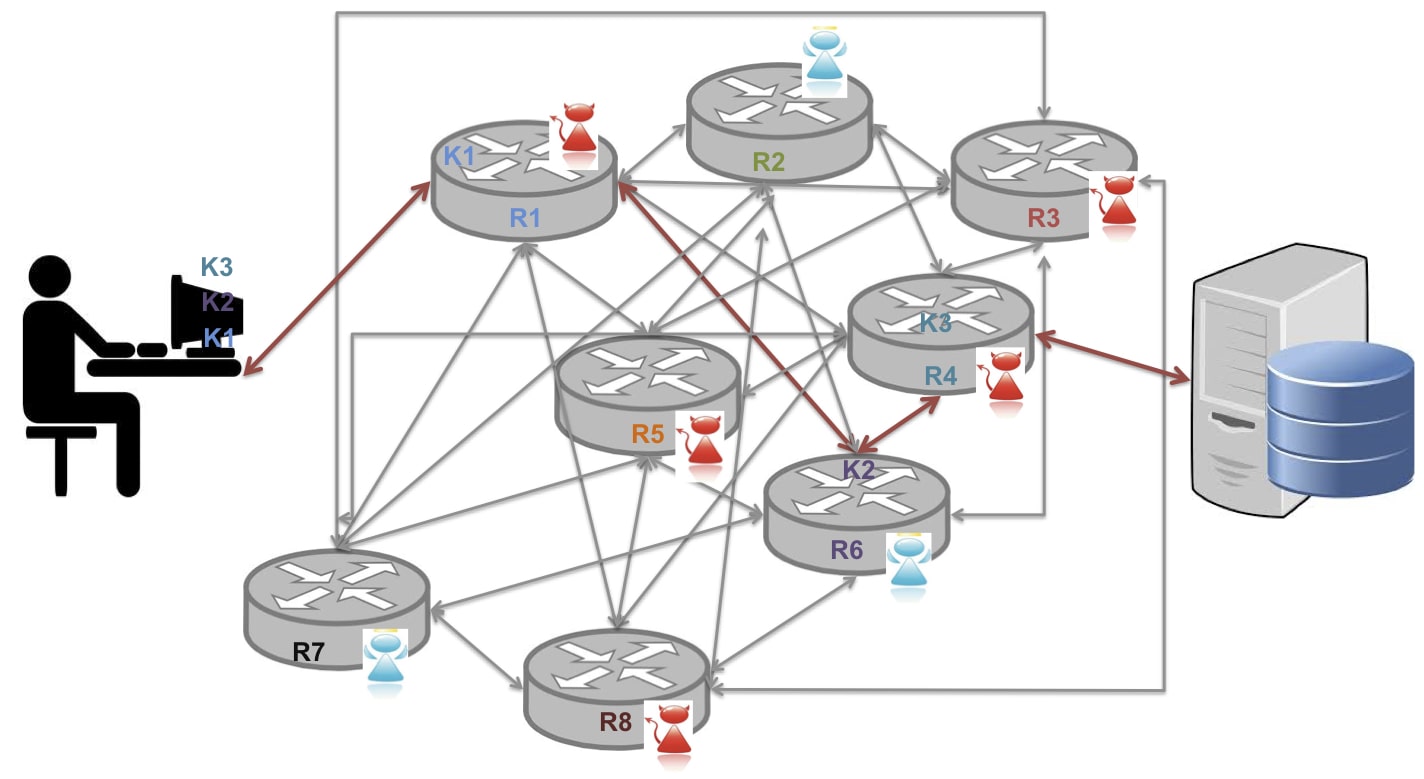
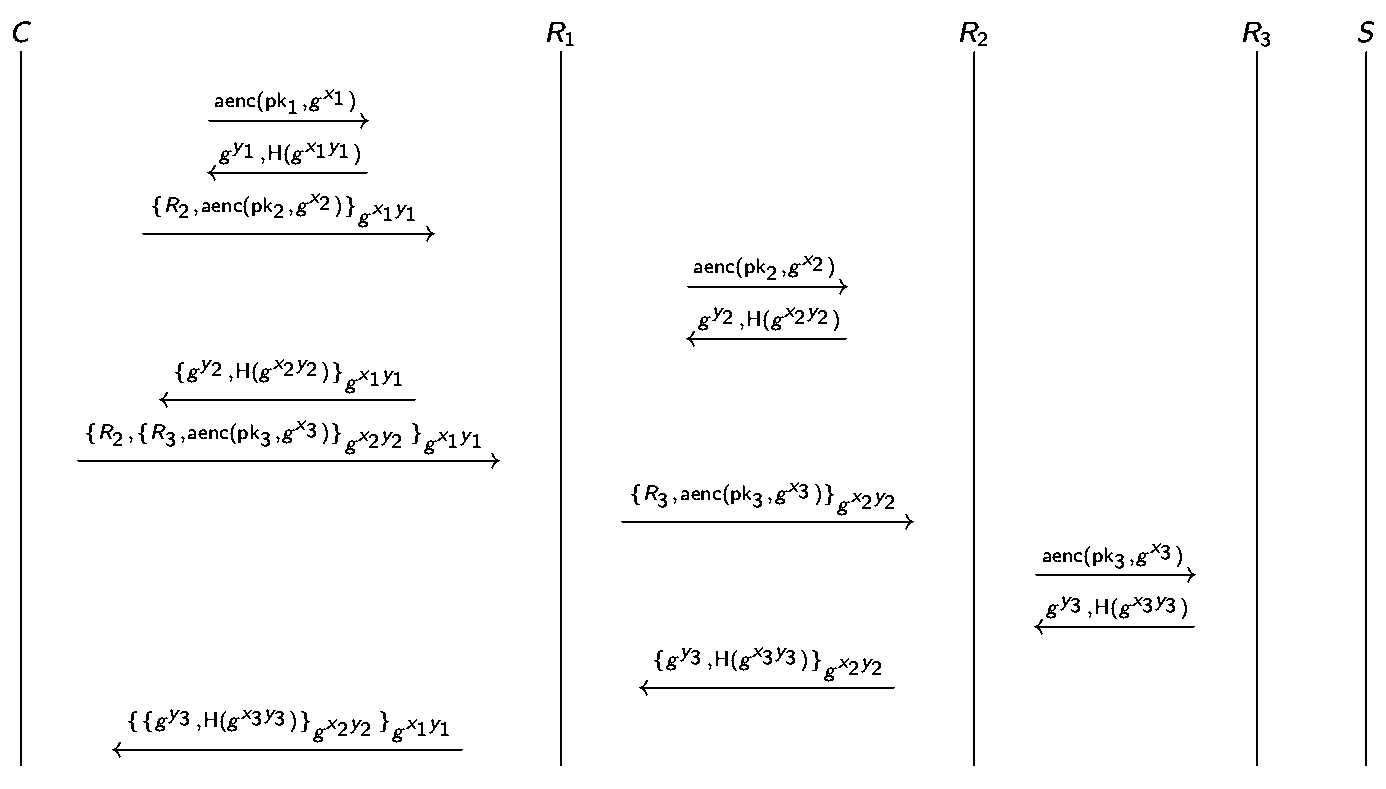
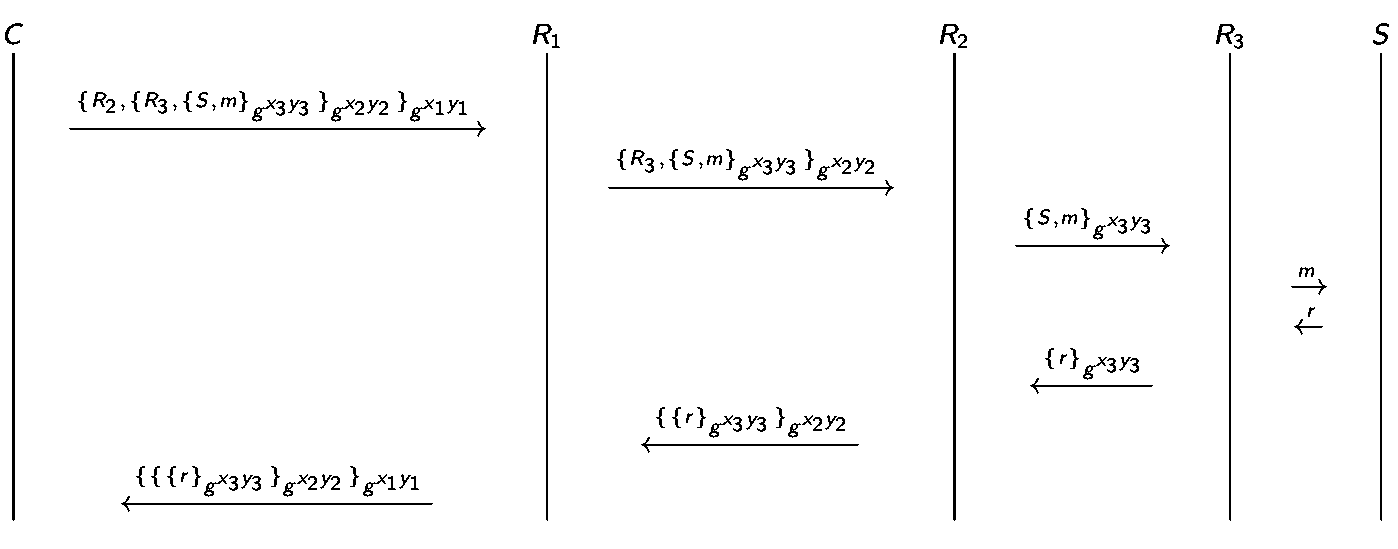
1. use public key crypto only to establish circuit while use symmetric key to exchange data
2. provides privacy not confidentiality: only anonymize the origin of the traffic and encrypts everything inside the TOR network but does not encrypt all traffic through the Internet. Confidentiality still requires to use end-to-end encryption such as TLS.
3. delegates DNS resolution to the exit node
4. TOR bridge relays which are not listed in the public TOR directory can prevent the ISPs from blocking access

Limitation: not secure against end-to-end timing attacks, i.e., if the attacker can see both ends of the communication channel, he can correlate volume and timing information on the two sides.